01
债券久期
1.久期的概念
久期(Duration)是指市场收益率变动一个百分点时,债券组合价值的波动幅度。它用来衡量债券组合对于利率变动的敏感性。
久期的概念最早是麦考利(Macaulay)在1938年提出来的,所以又称麦考利久期(简记为D)。麦考利久期是使用加权平均数的形式计算债券的平均到期时间。它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。
具体的计算是:将每次债券现金流的现值除以债券价格得到每一期现金支付的权重,并将每一次现金流的时间同对应的权重相乘,最终合计出整个债券的久期。因此,麦考利久期的单位是年。
麦考利久期公式:
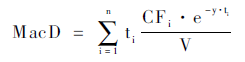
MacD表示麦考利久期;
ti表示i次现金流的时间;
V表示债券价值;
CFi表示第i次现金流的数量;
y表示收益率。
久期的计算公式就是一个加权平均数的公式,因此可以被看成收回成本的平均时间。
案例1
麦考利久期计算示例。
有如下债券(如表1和表2所示):
表1 债券信息简要
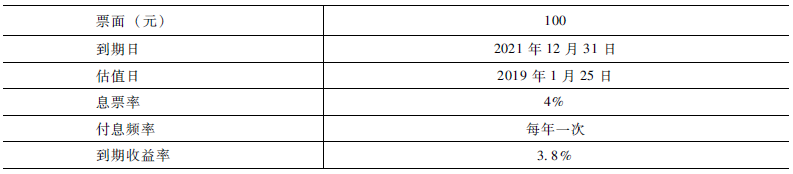
表2 债券现金流
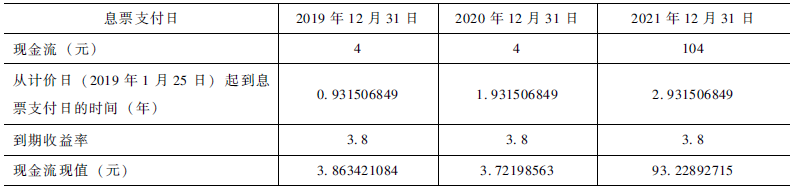
麦考利久期=
(3.863421084×0.931506849+3.72198563×1.931506849+93.22892715×2.931506849)÷债券全价=2.8179(年)
2.修正久期
在实际的债券分析中,久期已经超越了时间的概念,投资者更多地把它用来衡量债券价格变动对利率变化的敏感度,即衡量当收益率变化到一定程度时,债券价格变化多少,并且经过一定的修正,使其能精确地反映量化利率变动给债券价格造成的影响。由此,我们就有了修正久期这个概念。
修正久期公式:
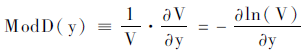
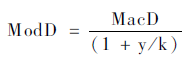
k是一年付息次数;
V是债券价格;
y是收益率。
修正久期的计算:
在【案例1】中,债券的修正久期是多少?
修正久期=麦考利久期/(1+收益率/付息频率)=2.7148。
修正久期是债券价格对收益率的一阶导数,其经济含义可以理解为,假如修正久期是5,当收益率下降1%时,债券价格上升5%。
修正久期越大,债券价格对收益率的变动就越敏感,收益率上升所引起的债券价格下降幅度就越大,而利率下降所引起的债券价格上升幅度也越大。可见,同等要素条件下,修正久期小的债券比修正久期大的债券抗收益率上升风险能力强,但当收益率下降时,收益能力较弱。
正是久期的上述特征给我们的债券投资提供了参照。当我们判断当前的利率水平存在上升可能时,就可以集中投资于短期品种、缩短债券久期;当我们判断当前的利率水平有可能下降时,则拉长债券久期、加大长期债券的投资,这就可以帮助我们在债市的上涨中获得更高的溢价。
久期可以带来债券投资管理中的一个极其重要的策略——“免疫策略”的理论基础,根据该策略,当交易主体债券组合的久期与债券的持有期相等的时候,该交易主体短期内就实现了“免疫”的目标,即短期内的总财富不受利率波动的影响。原理即把债券组合久期调整为0,这样收益率变动就不会影响债券的价值。
02
债券的凸性
我们之前介绍了衡量债券价格对收益率变化敏感程度的指标久期,使用久期的确能较好地近似衡量收益率变化时债券价格大致变化了多少。但是,当收益率发生较大变化时,使用久期来计算债券价格的变化会有一定误差,比如表3中提到的债券:
表3 债券信息简要
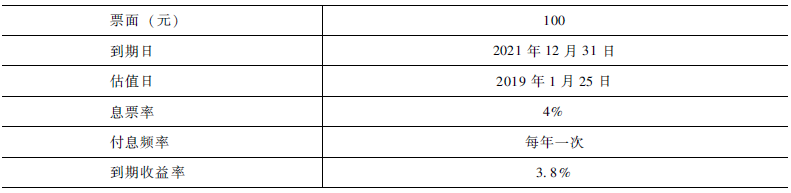
我们知道其修正久期为2.7148,全价为100.8143元。如果收益率上升10个基点,即从3.8%上升到3.9%,重新计算的债券价格是100.5412元。按照久期调整的价格是
100.8143-0.1%×2.7148×100.8143=100.5406元,两者之间差距不大。如果收益率上升100个基点,即从3.8%上升到4.8%,重新计算的债券价格是98.1278元。按照久期调整的价格是
100.8143-1%×2.7148×100.8143=98.0774元,有5分的差距。
从上述例子中可以看出,当收益率发生大规模移动时,使用久期来计算债券价格的变化会有一定误差,其原因是久期本身也会随着收益率变化,因此为了更精准地衡量债券收益率变化对债券价格造成的影响,我们需要引入一个新的概念,凸性。
债券的凸性是1984年斯坦利·迪勒(Stanley Diller)提出的概念,是对债券价格曲线弯曲程度的一种度量。严格地讲,凸性是指债券到期收益率发生变动而引起的债券价格变动幅度的变动程度。凸性是债券价格对收益率的二阶导数。凸性越大,债券价格曲线弯曲程度越大,用修正久期度量债券的利率风险所产生的误差越大。凸性也是债券久期对利率敏感性的测量。在价格—收益率出现大幅度变动时,它们的波动幅度呈非线性关系。由久期做出的预测将有所偏离。凸性就是对这个偏离的修正。
债券的凸性有以下几点特征:
(1)凸性随久期的增加而增加。若收益率、久期不变,票面利率越大,凸性越大。
(2)对于没有隐含期权的债券来说,凸性总大于0,即利率下降,债券价格将以加速度上升;当利率上升时,债券价格以减速度下降。
(3)含有隐含期权的债券的凸性一般为负,即价格随着利率的下降以减速度上升,或债券的有效持续期随利率的下降而缩短,随利率的上升而延长。因为利率下降时买入期权的可能性增加了。
案例2
假如一个债券的久期是5,凸性是30,如果收益率上升100基点,那么债券价格的变化是:
-5×(1%)+1/2×30×1%×1%=-4.85%,价格下跌幅度比只用久期的计算(-5×1%)=-5%要低0.15%,那就是凸性的效果。
如果收益率下降100基点,那么5×(1%)+1/2×30×1%×1%=5.15%,价格上涨幅度比只用久期的计算(5×1%)=5%要高0.15%。
通过案例2可以验证,正凸性会导致债券价格在收益率下降时价格上升的幅度超过相同收益率上涨幅度时带来的价格下跌幅度。


