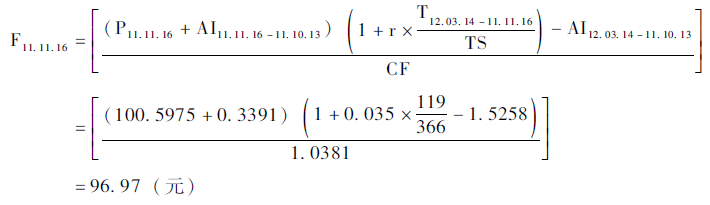同其他期货一样,国债期货的定价也是从现货价格出发,需要考虑资金成本,持有损益。同其他期货不同的是,国债期货需要考虑转换因子。
期货价格=(现货价格+融资成本-持有收益)/转换因子
国债期货的定价公式是:
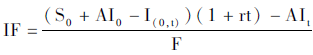
其中:
S0是最便宜可交割券在0时刻的净价;
AI0是0时刻应计利息;
I(0,t)是0到t时刻付出的利息的现值;
AIt是t时刻应计利息;
F是转换因子;
r是对应(0,t)的无风险利率;
t是国债期货交割时间。
从上式中我们可以看出,国债期货的价格受到最便宜可交割券的影响,主要影响因子就是最便宜可交割券的净价、交易日的应计利息、交割日的应计利息、在交易日到交割日这段时间内的利息收入和转换因子。其中,债券的净价、应计利息等债券的信息都是当最便宜可交割券确定时就可以确定的,而无风险利率是参考市场上的国债或者回购利率,转换因子是由国债期货的合约到期日和最便宜可交割券确定的。因此,国债期货的价格就是由最便宜可交割券确定的。
案例
11附息国债21:票面利率为3.65%,2011年10月发行的7年期国债,到期日2018年10月13日。其距离2012年3月14日交割日约6年半,符合可交割国债条件。
我们假设当前日期为2011年11月16日,11附息国债21的报价为100.5975元,TF1203国债期货报价为96.68元。
由于该债券年付一次利息,最近的一次附息日(该例中为起息日)是2011年10月13日,至11月16日,应计利息为0.3391元。
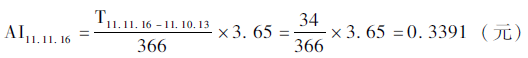
由于11附息国债21的报价为净价,即去掉未付的应计利息,我们得到2011年11月16日11附息国债21的全价为:
100.5975+0.3391=100.9366(元)
转换因子的计算(CF为到期收益率为3%,面值为1元的可交割债券的净价):CF=1.0381。
其中:可交割国债的票面利率c=3.65%,名义标准券的票面利率y=3%,交割日距离下一次最近付息日的时间d=213天,计息周期天数TS=366天,n=7年(如下图所示)。

图 国债运行周期示意
由贴现因子的性质,我们基于在2011年11月16日的现货价格和期货价格,得到:
调整后的期货价格=96.68×1.0381=99.72元,调整后的现货价格=100.5975/1.0381=96.9054元。
由调整后的估值,我们可得11月16日,现货价格高于期货价格,基差为正。
基差=现货价格-期货价格×转换因子=0.8775。
在持有成本模型中,我们假设11附息国债21为最便宜交割债券。通过之前的假设以及计算数据,我们得到:
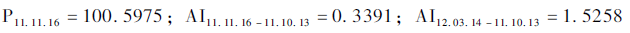
同时,我们假设无风险利率r=0.035,得2011年11月16日,TF1203期货合约的理论价格为:
期货价格=现货价格+融资成本-持有收益,即: