股指期货期现套利成功的一个前提是,投资者能够确定股指期货合约当前价格与现货指数差价是否合理,也就是判断两者之间是否存在套利空间。
目前,世界金融期货市场上进行期现套利决策的一个经常被使用的工具是利用股指期货的理论定价模型,通过对比股指期货的实际价格和理论价格来判断是否存在套利机会:
当实际价格高于理论价格时,卖空指数期货,买入指数现货;
当期货实际价格低于理论价格时,买入指数期货并卖空指数现货。
那么这个理论定价模型是怎么产生的呢?
经济学中有个基本定律称为“一价定律”。意思是说,两份相同的资产在两个市场中的报价必然相同,否则一个市场参与者可以进行所谓无风险套利,即在一个市场中低价买进,同时在另一个市场中高价卖出;最终,原来定价低的市场中因对该资产需求增加而使其价格上涨,而原来定价高的市场中该资产价格会下跌,直至两个报价相等。因此,供求力量会产生一个公平而有竞争力的价格以使套利者无法获得无风险利润。
根据上述定律,股指期货合约的价格与现货指数价格之间的差价在理论上应该处于一个合理范围。也就是说,投资者可以根据股票现货价格计算出股指期货价格在理论上的合理价位。于是,股指期货的理论定价模型应运而生。
01 股指期货理论定价模型的推导
由于影响股指期货价格的相关因素太多,无法设立包罗所有影响因素的数学模型,因此,只能筛选出主要影响因素来建立数学模型。
1.股指期货是从股票指数衍生而来,因此,它的价格(F)与股票现货指数的价格(I)戚戚相关。股票现货指数价格的涨跌必然影响股指期货价格的涨跌。由此可以建立以下最粗糙的数学模型:
F~I
其中:符号~代表相关性。
2.我们需考查在买卖过程中影响股指期货价格的主要因素。我们发现,由于期货有交割期,卖方要过一段时间后才能交付现货得到现金,买方到交割时才付出现金交收现货,相当于买方向卖方融资。这个融资成本用该时段的无风险利率(可以考虑用市场利率代替)R表示。这样,当卖方卖出期货合约时,他需要得到相当于在交割前向买方“融资”的收益I·R。这个收益应该加在期货价格F里。于是我们将原始的数学模型进一步精确化:
F≈I+I·R
小贴士
无风险利率
无风险利率,是指将资金投资于某一项没有任何风险的投资对象而能得到的利息率。这是一种理想的投资收益率。在证券市场上,无风险证券的利率为无风险利率。无风险证券是指能够按时履约的固定收入证券,即没有任何风险的证券。
在证券界通常将期限小于3个月的短期贴现国债视为无风险证券。这是因为3个月的期限很短,在这期间市场利率波动对债券的影响很小,其收益基本是恒定的,可以认为是没有风险的。我国目前还没有3个月的国库券,因此无风险利率可以参照一年期存款利率。
3.我们还发现股票有分红机会,这是影响股指期货价格的第三大因素。期货卖方虽然卖出了股指合约,相当于把股票组合提前卖掉了,但在交割期到来前,仍持有股票组合,还可以收到股息,因而减少了其持仓成本,这对相当于已经买了这个股票组合的期货多头来说不太公平,因此期货价格要向下调整相当于股息的幅度。设股息率为D,结果期货价格还应减去对应资产收益I·D:
F=I+I·R-I·D
4.期货合约交割时间的长短是影响期价的第四大因素。因为不同交割时间越长,相当于融资时间越长,就像定期储蓄一样,钱存的时间越长,利息越高,所以不同月份的期货合约挂牌价应存在不同的时间升水问题。设期货合约的交割期为T-t日,化为年份为(T-t)/365,最终股指期货理论定价模型为:
F=I+I·R·(T-t)/365-I·D·(T-t)/365
即:
F=I+I·(R-D)·(T-t)/365
其中:F——股指期货理论价格;
I——现货股指价格;
R——无风险利率;
D——年股息收益率;
T——交割时间;
t——某一时间。
5.其他影响因素怎么办?这些因素全部被假定处于理想条件下,因此不再在模型中予以考虑。这些次要因素被假定为:
①投资者构造出的投资组合与股市指数在组合比例、股指的价值与股票组合的市值方面都完全一致;
②投资者可以在金融市场很方便地借款和贷款以用于投资;
③无交易费用;
④当套利机会出现时,市场参与者将参与套利活动;
⑤无心理恐慌因素;
⑥对股指期货合约进行现金结算。
6.如果考虑用连续复利形式的R、D,则上述股指期货的理论定价模型将更精确为:
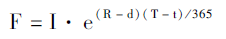
其中:R——无风险利率;
d——以连续复利计算的年股息收益率(%);
T——期货合约到期时间;
t——现在的时间;
T-t——期货合约到期天数。
02 连续复利下的股指期货理论定价模型的推导
首先要解决什么是复利。
案例
设100元钱投资一年,年利率10%,如果年底一次性发放红利,则:
本利=100×(1+10%)=110.00(元)
如果每半年发放一次红利,则:
上半年本利=100×(1+10%/2)=105(元)
年底本利=105×(1+10%/2)=110.25(元)
改为连续式:
年底本利=100×(1+10%/2)×(1+10%/2)
=100×1.05×1.05=110.25(元)
多出的0.25元就是利滚利带来的,称为“复利”。
那什么是连续复利呢?我们来看看提高计算复利的频率对100元在一年末的价值影响(见表1)。
表1 提高计算复利的频率对100元在一年末的价值影响
(设利率为每年10%)
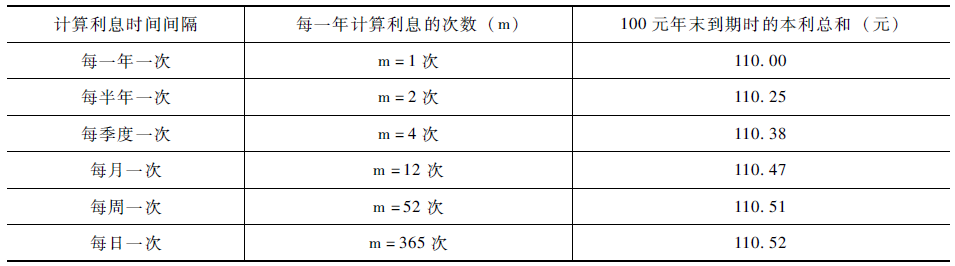
当m趋于无穷大时,就称为连续复利。
我们发现,当计算利息时间间隔达到每周一次和每日一次时,当m趋于无穷大时,年末到期时的本利总和已相差无几了。从实用性来看,通常认为连续复利与每日计复利等价。
根据连续复利的概念我们来推导下面的公式。
公式推导:由
F=I+I·(R-D)·(T-t)/365
=I·[1+(R-D)·(T-t)/365]
设:i=(R-D)·(T-t)/365
则:F=I·(1+i)
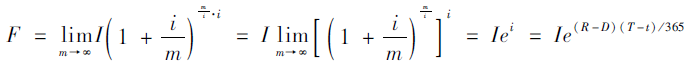
有了上述理论定价模型,我们就可以随时计算出当时股指期货合约的理论价格,然后与股指期货合约实际价格对比。当股指期货合约实际价格高于或低于股指期货合约理论价格时,进行套利交易可以盈利。但事实上,交易是需要成本的,如交易手续费、资金利率成本等。这导致正向套利的合理价格要向上移,反向套利的合理价格要向下移,形成一个区间。在这个区间里,套利不但得不到利润反而会导致亏损,因为所套的利润还不够交纳交易成本费用。这个区间称为“无套利机会区间”(也称“套利成本区间”)。只有当期货指数实际交易价格高于区间上界时,正向套利才能进行;反之,当期货指数实际交易价格低于区间下界时,反向套利才能进行。
现在的关键是如何确定这个无套利机会区间的上下限,这是期现套利成功与否的重要一环。
03 无套利机会区间上下限的确定
案例
8月22日,股票市场上现货沪深300指数为1224.1点,当年A股市场分红年股息率在2.6%左右,假设融资(贷款)年利率r=6%,那么,10月22日到期交割的股指期货10月合约的目前理论价格应为:
F=1224.1+1224.1×(6%-2.6%)×1/6=1231.04(点)
据此来计算股指期货合约的无套利区间。
又假设:投资人要求的回报率与市场融资利差为1%;期货合约的交易双边手续费为0.2个指数点;市场冲击成本为0.2个指数点;股票交易双边手续费及市场冲击成本为1%。折算成指数点是:
借贷利率差成本=1224.1×1%×2/12(年份)=2.04(点)
股票交易双边手续费及市场冲击成本=1224.1×1%=12.24(点)
期货交易双边手续费及市场冲击成本=0.2+0.2=0.4(点)
合计(TC)=12.24+2.04+0.4=14.68(点)
前面已经求得目前股期期货合约的合理价格应为1231.04点,那么:
套利区间上界=1231.04+14.68=1245.72(点)
套利区间下界=1231.04-14.68=1216.36(点)
无套利机会区间=[1216.36,1245.72]
也就是说,在8月22日沪深300现货指数为1224.1点时,股指期货10月合约的价格如果在1245.72点以上时进行正向套利或者在1216.36点以下时进行反向套利才会有盈利,而且10月合约涨得越高正向套利盈利空间越大,跌得越低反向套利盈利空间越大或越安全。而10月合约价格在[1216.36,1245.72]内是无套利机会的。
小贴士
市场冲击成本
市场冲击成本,是指在套利交易中需要迅速而且大规模地买进或者卖出股票时,未能按照预定价位成交,从而多支付的成本。例如:投资者以每股15.50元挂盘买入小盘股“海欧卫浴”,但无法成交。此时市场挂出的卖盘价为15.70元/股,而整个市场在上涨,该投资者担心买不到,最后不得不以15.70元/股价买到股票,使得购股成本每股多支付了0.20元,这就是冲击成本。再比如,某只基金的现价为1.10元,而投资者为了保证买入交易成功,很可能以1.11元成交,高出现价0.01元的费用便是市场冲击成本。
各国证券市场的数据表明,市场冲击成本一般为佣金与税收的2倍以上。冲击成本被认为是机构大户难以摆脱的致命伤。比如,机构大户看好一组股票时,必须花费很长时间才能实现自己的建仓目的。如果急于建仓,由于短时间内大量买进会抬高股价,势必会使建仓的成本远高于预期成本。同样,如果急于抛股,等于是自己在打压股价,最后实现的卖出价低于原来的预期价格。对散户而言,由于买卖交易量很小,冲击成本几乎为零。
冲击成本的大小,既与委托交易的数量有关,也与流动性大小有关。市场的流动性越小,冲击成本越大。股票市场上每天的成交金额有几百亿元,看上去规模不小,流动性也可以。但那是上千只股票共同交易的结果,如果细分到不同的个股,不难发现其中一些股票的流动性还是很差的。相对而言,买卖股指期货的冲击成本就非常小。这是因为相应的股指期货合约只有几个,交易集中导致流动性非常强,即使是机构大户,在其中进出也很方便。


