一手国债期货和现货的票面金额是100万元，进行国债基差交易需要大量的资金，当资金量不足的时候，如何进行基差交易呢？这里介绍几种降低资金需求量的方法。

我们知道，在国债基差交易中，期货的数量是CF份。期货和现货的数量必须是整数，因此需要将期货现货数量等比例放大到最接近的整数。转换因子CF的小数部分越复杂，为了进行期货现货数量的最佳匹配，需要的资金量就越大。

一般情况下，转换因子的小数部分都是非常复杂的，令期货现货的数量完全匹配，需要非常多的期货和现货，资金需求量也十分巨大。为了降低转换因子的复杂性，可以采用将转换因子近似处理的方法。

案例1

如果某国债现货的转换因子是1.22，期货现货比例1.22:1＝61:50，即最少准备61张期货、50张现货合约，对应的市值约为6100万元和5000万元。期货的资金只需要缴纳保证金即可，按2%计算，期货方面最少需要约122万元资金。现货方面需要支付全额资金，即5000万元。总资金需求为5122万元。

如果将转换因子近似为1.2，期货现货比例1.2:1＝6:5，则只需要6张期货和5张现货，对应市值分别是610万元和500万元，所需资金分别是12万元和500万元，总资金需求为512万元。

我们将1.22近似为1.2，仅仅进行了一点调整，便将资金量从5122万元降至512万元，总资金需求降低了90%。可见，将转换因子进行近似处理，可以达到降低资金需求的效果。

因为期货数量是近似的结果，所以会出现风险敞口，具体的计算在前面章节有详细介绍，这里就不重复了。严格地讲，现实中的基差交易都会存在风险敞口，区别只是敞口大小不同。

既然如此，我们可以将所需的资金量压到最低，将转换因子近似为1，进行期货数量和现货数量都是1手的基差交易。这种情况下，现货只需要100万元即可，总资金需求约为102万元。

这是一种比较极端的情况，存在一定的风险，但并非不能盈利。为便于区分，我们将期货现货数量1:1的交易形式叫做“价差交易”。同普通的基差交易一样，结束价差交易的方式有进入交割和提前平仓两种，下面我们分别来计算损益。

进入交割：以做空期货、做多现货的价差交易为例，在T1开始交易时，期货现货价格分别是F1和B1，在T2交割时刻期货现货价格分别是F2和B2，期货现货数量始终是1，则在不考虑交易成本的情况下，总损益是：

-(F2-F1)＋(B2-B1)＋carry＋(F2×CF-B2)

＝-(F2-F1)×CF＋(F2-F1)×(CF-1)＋(B2-B1)＋carry＋(F2×CF-B2)

＝(F1×CF-B1)＋(F2-F1)×(CF-1)＋carry

＝carry-basis1＋(F2-F1)×(CF-1)

提前平仓：以做空期货、做多现货为例，在不考虑交易成本的情况下，总损益是：

-(F2-F1)＋(B2-B1)＋carry

＝-(F2-F1)×CF＋(F2-F1)×(CF-1)＋(B2-B1)＋carry

＝(B2-F2×CF)-(B1-F1×CF)＋(F2-F1)×(CF-1)＋carry

＝basis2-basis1＋carry＋(F2-F1)×(CF-1)

不管是进入交割还是提前平仓，价差交易都比普通基差交易多了(F2-F1)×(CF-1)的部分。当CF非常接近1的时候，价差交易与基差交易的损益相差无几。当CF与1相差较大的时候，价差交易与基差交易哪个盈利更高，取决于(F2-F1)×(CF-1)是正值还是负值。

对于进入交割的情况，因为基差一般会大于持有收益，所以基差交易进入交割是发生亏损的，但价差交易当行情与CF合适时，是有可能盈利的。对于提前平仓的情况，基差多头交易提前平仓的前提是已经有了浮动盈利，因此只要(F2-F1)×(CF-1)不是亏损非常大，整体的交易还是可以盈利的。

案例2

在2012年12月28日，国债100002的到期收益率是3.3%，价格是100.8146元，票息3.43%，对TF1303合约的转换因子是1.0266，期货TF1303合约的价格是97.908元。

当前市场收益率处于较高水平，我们认为未来收益率水平会下降。但是，因为资金量不足，不能进行期现数量1.0266:1的基差交易，所以进行价差交易，买入现货，卖出期货。

到了2013年3月8日，收益率下跌至3.1%，国债100002的价格上涨至102.0353元，期货价格上涨至99.292元，进入交割。

在2012年底开始交易时，国债100002的基差是100.8146-1.0266×97.908＝0.3（元）。国债的票息3.43%，融资成本2%，则持有收益是(3.43%-2%)×100×(70/365)＝0.2742（元）。价差交易与基差交易的差值部分是(1.0266-1)×(99.292-97.908)＝0.0368（元）。则总损益是：0.2742-0.3＋0.0368＝0.0110（元）。

如果按期货数量是1.0266份进行基差交易，基差的损益是0.2742-0.3＝-0.0258（元），是亏损的。价差交易提高了原本的基差交易的绩效。

利用价差交易，可以最大限度地减少资金使用量，但由于期现数量没有完全匹配，存在一定的风险敞口。

有没有既能够降低资金需求，又不承担数量不匹配造成的风险的方法呢？答案就是国债现货的正回购操作。国债正回购可以将国债现货的头寸放大，实现杠杆化操作。因为有部分现货是被质押的，所以不能进入交割环节。

假设进行正回购操作，将国债的数量放大K倍，也就是说购买现货需要的资金量降低至正常资金需求的1/K。

案例3

以【案例5-23】中的数据为例，在转换因子从1.22近似为1.2时，期货和现货的数量分别是6手和5手，总资金量需求是512万元。

如果在现货方面进行正回购操作，放大倍数为5倍，则实际只需要100万元资金购买现货即可。期货的资金需求仍然是12万元，因此总资金需求量是12＋100＝112万元，较没有进行正回购的时候，资金量降低了78%。

显然，正回购将现货放大的倍数越多，资金的实际需求量越少。在现实中，国债的正回购操作会有一定的限制。具体操作可以参考相关的交易制度。需要注意的是，进行正回购操作时，现货的价格使用的是全价计算，而不是净价。

下面我们来计算现货上进行正回购操作的基差交易的损益情况。在基差交易开始前，先要对现货进行循环的正回购操作，整个正回购基差交易的流程如图1所示：

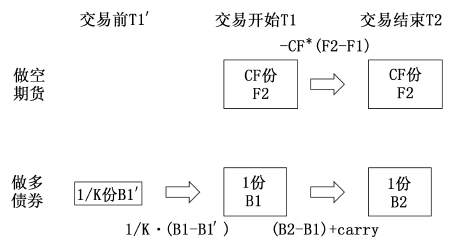
图1 结合国债正回购的基差交易

进行循环的正回购操作后，现货放大了K倍，则总损益是：

-CF×(F2-F1)＋1/K×(B1-B1′)＋(B2-B1)＋carry

＝(B2-CF×F2)-(B1-CF×F1)＋1/K×(B1-B1′)＋carry

当T1′与T1十分接近的时候，B1′与B1近似相等，则上述结果可以简化为basis2-basis1＋carry。

需要注意的是，这里的carry与前面章节的carry有所不同。之前计算持有收益时，购买现货的全部资金都是自有资金，资金成本计算比较简单。但在进行正回购操作时，购买现货的资金里面，只有一小部分是自有资金，其他资金是融资得到的，因此计算资金成本时，需要分别计算。

假设现货的票息是i，自有资金的资金成本是r，正回购的融资成本是c，则普通基差交易的持有收益是i-r，结合正回购的基差交易的持有收益是：

carry＝i-1/K×r-(K-1)/K×c＝i-r-(K-1)/K×(c-r)。

也就是说，结合正回购的基差交易，其损益会比普通基差交易损失(K-1)/K×(c-r)。

我们分别计算自有资金的成本r和正回购的融资成本c，是为了计算得更加准确。在实际情况中，往往使用正回购利率来计算自有资金成本，因此r＝c，此时普通基差交易的持有收益和结合正回购的持有收益是相同的。即便使用不同的资金成本来计算r和c，两者也相差不大，因此对基差交易的损益影响微乎其微。

虽然结合正回购的基差交易不能进入交割，但实际上对交易并不会造成很大影响。这是因为，普通的基差交易的盈利方式就是在基差扩大时提前平仓，将浮盈转换为实际盈利。因此，是否能进入交割环节，对盈利状态下的基差交易不会有任何影响。此外，如果持有基差多头到最后交易日，是否进行交割的差异只是期末时刻的基差。在一般的情况下，基差都会趋近于0，绩效差异会很小。

使用正回购的方法既可以节省大量的资金，又不会对基差交易的绩效产生很大的影响，是一种理想的减少资金需求量的方法。

我们介绍了三种降低资金量的方式，分别是：对转换因子进行近似处理，期货现货数量按1:1进行价差交易，现货结合正回购进行基差交易。

现实中的转换因子的小数部分通常比较复杂，因此实际的基差交易或多或少都进行了近似化的处理。将这种近似处理发挥到极致，就是价差交易。两种方法都存在一定的风险敞口。

正回购的方式可以和前两种方法结合使用，将资金需求量进一步压缩，且对绩效不会造成很大的影响，是一种比较理想的降低资金需求的方法。

正回购操作要循环进行，操作相对复杂，因此实际使用时需要注意中间的操作风险。另外，由于正回购操作将现货头寸进行了放大，对于实际资金量来说，收益和风险都进行了等比例的放大，当基差交易发生亏损时，亏损的比例会扩大。

在实际操作中，交易者需要根据实际的资金量和风险承受能力选择合适的操作方式。